
"켈리 공식"을 알면 투자에서 이길 수 있다?
Gufinance
·2024. 1. 4. 08:00

반갑습니다. 금융관찰자 'GUFI' 입니다.
오늘 Gufinance에서는 켈리 공식에 대해 분석합니다.
켈리 공식이란?
켈리 공식 혹은 탐욕의 공식으로도 알려진 켈리 공식은 투자자가 특정 자산에 투자할 최적의 금액을 결정하는 데 도움이 되는 수학적 방정식입니다. 이 공식은 1956년 미국의 수학자 J.L. Kelly가 발표한 공식으로, 나중에 이 공식은 도박이나 주식에 얼마나 많은 돈을 투자해야 하는지에 대한 방정식으로써 투자 이론의 길을 열었습니다.
이 공식은 최적의 베팅 규모는 당첨 확률과 잠재적 지불금 규모에 따라 달라진다는 아이디어를 기반으로 합니다. 이 공식은 특정 투자 기회에 할당해야 하는 투자 포트폴리오의 비율을 결정하는 데 사용할 수 있습니다.
켈리 공식의 도출
공식의 도출 과정은 다소 복잡할 수 있지만, 기본 개념은 주어진 투자 기회에 베팅할 투자 자본의 최적 비율을 찾는 것입니다. 이 공식은 승률, 지급률, 투자 가능한 총자본금을 고려합니다.
예를 들어 투자자가 투자할 수 있는 자본이 $10,000이고 두 가지 투자 기회를 고려하고 있다고 가정해 보겠습니다.
기회 A의 승률은 60%이고 배당률은 2:1
기회 B의 승률은 70%이고 배당률은 1.5:1입니다.
켈리의 공식을 사용하여 투자자는 각 기회에 대한 최적의 자본 배분을 결정할 수 있습니다.
기회 A와 B에 대한 최적의 배분을 계산하기 위해 켈리 공식을 사용한다면
공식
" F = (BP - Q) / B "
여기서
f = 투자자의 자본 중 기회 A에 베팅하는 비율
b = 배당률(A의 경우 2)
p = 승률(A의 경우 0.6)
q = 손실률(A의 경우 0.4)
이 예제의 값을 연결하면 다음과 같이 계산됩니다:
f = ((2 * 0.6) - 0.4) / 2 = 0.2 또는 20%
즉, 투자자의 자본을 기회 A에 최적으로 배분하는 비율은 20%입니다.
기회 B에 대한 최적의 배분을 계산하기 위해서도 동일한 공식을 사용하나 승률과 지불금 비율이 다르기에 결과도 달라집니다.
f = ((1.5 * 0.7) - 0.3) / 1.5 = 0.4 또는 40%
즉, 투자자의 자본을 기회 B에 최적으로 배분하는 비율은 40%입니다.
결론
켈리의 공식은 투자자가 파산 위험을 최소화하면서 수익을 극대화할 수 있도록 도와주는 자금 관리 기법입니다. 이 공식에 따라 투자하면 투자자는 가능한 가장 빠른 속도로 총자산을 늘릴 수 있습니다. 그러나 이 공식은 완벽하지 않으며 투자의 모든 가능성을 고려하지 않는다는 점(현실적으로 확률을 전부 고려하여 도출하기는 어려움)에 유의하는 것이 중요합니다.
명심해야 할 점은 켈리 기준은 각 결과의 실제 확률을 알고 있다고 가정한다는 것입니다. 실제로는 정확한 확률을 알 수 없으므로 투자자는 과거 데이터, 시장 동향 및 기타 요인을 바탕으로 추정해야 합니다.
그러나 켈리의 공식은 투자자가 다양한 투자 기회에 자본을 최적으로 배분하는 데 사용할 수 있는 강력한 도구입니다. 이 공식을 사용하면 투자자는 손실 위험을 최소화하면서 수익을 높일 수 있습니다. 그러나 이 공식은 다른 투자 전략과 함께 사용하고 투자 결정을 내리기 전에 항상 직접 조사해 확률을 정확히 계산하는 과정이 가장 중요합니다.
켈리 공식, 직접 구해보자


켈리 공식으로 최적 투자 비중을 도출할 때는 복잡한 수식을 넣을 필요 없이, 그저 승률, 수익률, 손실률만 기입하면 최적 투자 비중과 시뮬레이션 결과를 도출해 줍니다. 사이트는 다음과 같습니다.
켈리 공식 계산기 - Fical.net
켈리 공식 계산기는 주식이나 암호화폐의 최적의 투자 비율을 계산하는 도구입니다.
fical.net
참고
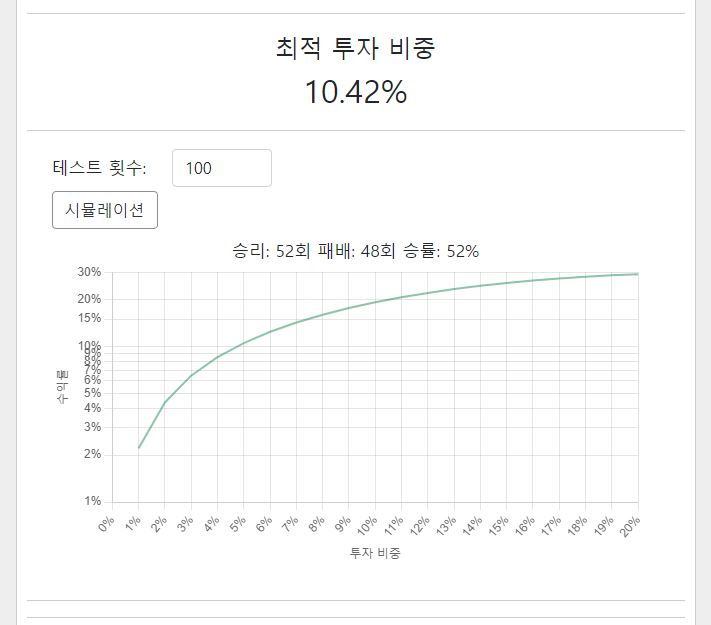
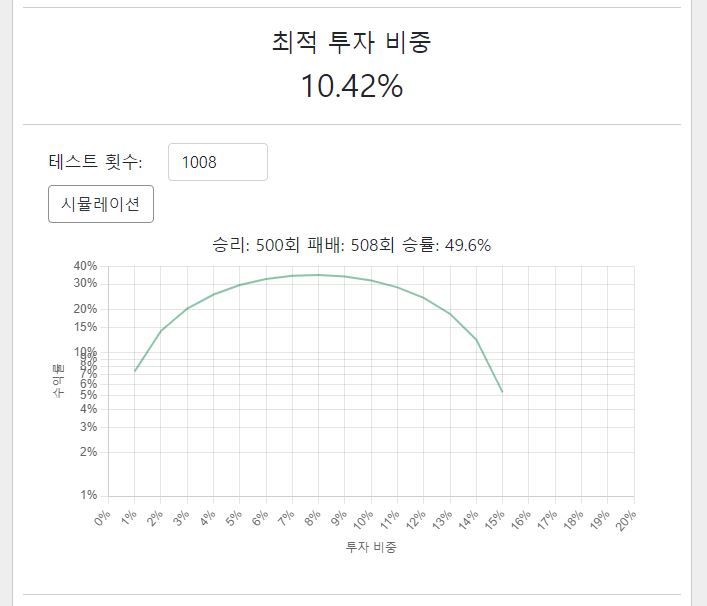
한편, 같은 투자 확률이라고 하더라도 시행 횟수, 실제 승률 결과에 따라 다른 결과가 나오기도 합니다. A와 B 시뮬레이션은 같은 확률을 대입했지만 실제 시뮬레이션 결과에서 B의 경우 A보다 저조한 성적을 내고 있습니다. 켈리 공식이 강력한 확률의 우위를 제공하지만, 100%의 승률을 가진 투자가 아닌 이상 손실의 확률, 언더 퍼폼의 가능성이 있다는 것을 염두해야 할 것입니다.
관련 링크
확률에 관한 타 게시물입니다.
마틴게일 베팅법, 장기적으로 파멸에 이르는 길.
반갑습니다. 금융관찰자 'GUFI' 입니다. 오늘 EI에서는 마틴 게일 베팅법의 개념, 위험성에 대해 분석합니다. 글을 열며 거래는 흥미롭고 수익성 있는 장기적 투자가 될 수 있지만 상당한 위험이
gufinance.tistory.com
이 글은 특정 종목에 대한 매수 및 매도 추천이 아니며, 투자의 책임은 모두 본인에게 귀속됨을 명시합니다.
구피넌스, GUFI 제공
'Financial Scope > MESSAGE - 투자' 카테고리의 다른 글
| 고PER은 싸고, 저PER은 비싸다 (0) | 2025.02.09 |
|---|---|
| TR 금지, ISA IRP 배당 혜택 몰수 대응방법 1 (0) | 2025.02.05 |
| "몬티홀 문제", 투자 습관에도 적용할 수 있다? (2) | 2024.01.01 |
| 중국 플러스 원 전략의 실현, 인도 투자 - Gufinance (1) | 2023.05.12 |
| 미국주식 시가총액 TOP 10 ( 2023. 05.01, 고화질 로고 ) (0) | 2023.05.01 |






